Quantum computing
Phase manipulation in quantum cryptography
Direct link to article: arxiv.org
The study bases on a geometrical phase associated to the Schrödinger equation in a three level system. When two Stimulated Raman Adiabatic Passage (STIRAP) processes are applied in a row; first the counterintuitive process and then the intuitive order process, the population is transferred back to the initial quantum state. The phase of the new state can be well controlled.
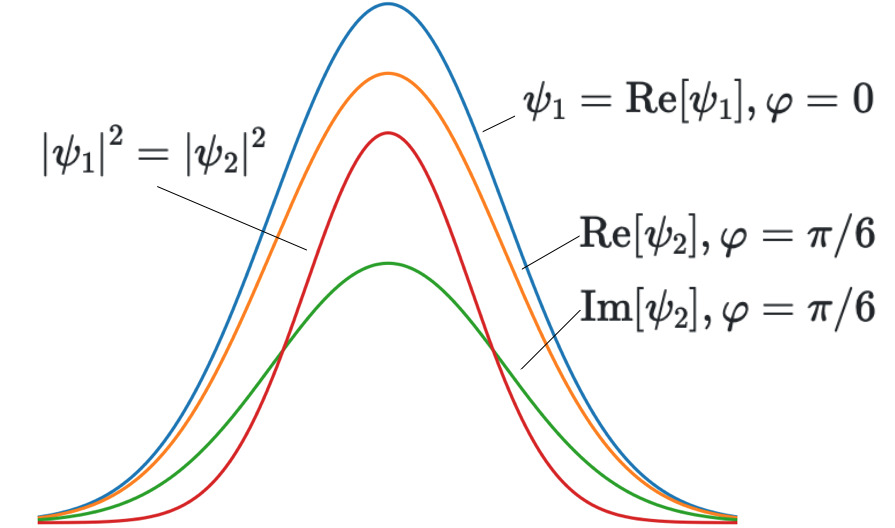
As an example, let's assume we have two states; the initial state \(\psi_1(x) \), the final state \(\psi_2(x) \) and the time shift between the laser pulses is \( \Delta T = 1/6 \). After the quantum transitions, the final state has obtained a phase \(\psi_2(x) = \psi_1(x)\exp(i\pi/6) \). The probabilities of the wave functions are the same \(|\psi_1|^2 = |\psi_2|^2\), but the quantum state is different. The situation is shown in the enclosed figure.
The applications include, for example, phase manipulation in quantum cryptography, phase gates in quantum computing and phase interactions in quantum interference. More details are found here.
Quantum computing - Hadamard gate
Direct link to article: arxiv.org
A quantum logic gate is a basic quantum circuit operating on a small number of qubits. The Hadamard gate acts on a single qubit. It represents a rotation of \(\pi \) about the axis at the Bloch sphere. In quantum optics, the Hadamard gate can be constructed using 4 levels as shown in the following figure.
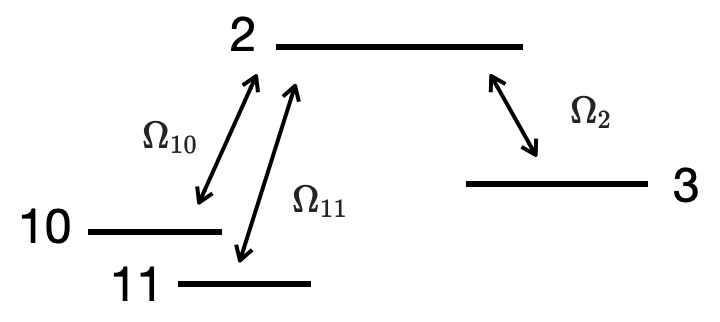
There are three couplings \( \Omega_{10} \), \( \Omega_{11} \) and \( \Omega_{2} \) which connect the levels. The initial population is either on levels \( |10 \rangle \) or \( |11 \rangle \). In the following section we show some exact solutions to the Hadamard system.
Monopoles and confinement
Direct link to article: arxiv.org
We show some visual images of the population transfer in the STIRAP system when the pulse areas are finite. This is the case when the magnetic monopoles are present.
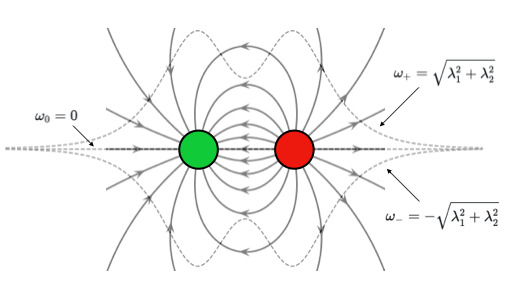
More details are found here.
Back to the main page.