Phase manipulation in quantum cryptography

Direct link to article: arxiv.org

We show an example of the optical phase manipulation.

Stimulated Raman adiabatic passage (STIRAP) is a process that transfers of a population between two quantum states via two coherent electromagnetic pulses. Here we consider an example of two concequtive STIRAP processes. The first counterintuitive STIRAP process transfers the population from level 1 to 3, and the other STIRAP is applied in the reverse order (intuitive order), in which the population is transferred back from state 3 to 1. The couplings between the levels are \(\Omega_1\) and \(\Omega_2\).

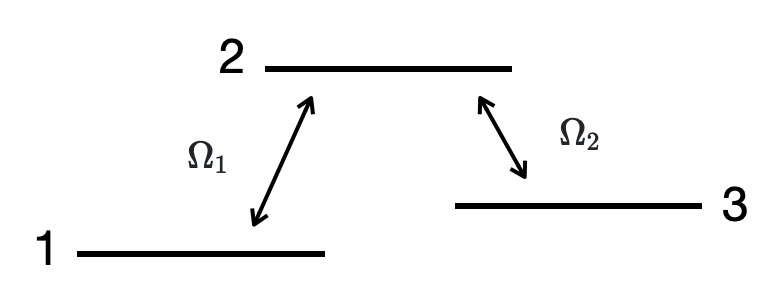
We consider the Schrödinger equation \begin{equation} i\hbar\frac{\partial}{\partial t} \Psi(R,t) = H_{3D}\Psi(R,t), \end{equation} where the Hamiltonian is
\begin{equation} H_{3D} = \left[ \matrix{ T_1(p)+V_1(x) & \Omega_1(t) & 0 \cr \Omega_1(t) & T_2(p)+V_2(x) & \Omega_2(t) \cr 0 & \Omega_2(t) & T_3(p)+V_3(x) \cr } \right]. \end{equation} Here \(T_i\) is a kinetic energy, \(V_i\) is a potential energy and \(\Omega_i\) is a coupling between the states. We choose a normalized minimum wave function which propagates in an harmonic oscillator potential \begin{equation} V \sim \frac{1}{2}m\omega^2x^2. \end{equation} The couplings \(\Omega_1\) and \(\Omega_2\) are applied in a counterintuitive and reverse (intuitive) order.

\( A \) is the pulse height, \( T \) is the pulse width and \(\Delta T\) is a time between the pulses. The final state on the level 1 is then \begin{equation} \tilde{\psi}_1(x) = \psi_1(x) e^{i\pi\Delta T}. \end{equation} The population is the same as in the initial quantum state on the level 1, but the wave function has obtained an additional phase \(\Delta T\). When the pulse areas are finite, the populations on the levels oscillate due to the Rabi cycle. One can tune the parameters \( AT \) and \(\Delta T\) in order to get a maximum transition between the states.

Generally, the measurement destroys the quantum state and the wave function cannot be changed. However, in our example we are able to manipulate the phase of the wave function and the state is not destroyed. This has applications, for example, in quantum cryptography and in quantum computing . More details and discussions can be found from the reference paper.

More topics on Quantum computing.